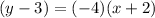Answer:
Explanation:
We know that the equation of a line in point-slope form that is passing through a point (a,b) and has slope m is given by :-
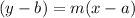
Then, the point-slope form of a line with slope -4 that contains the point (-2,3) :-
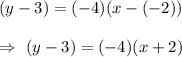
Hence, the point-slope form of a line with slope -4 that contains the point (-2,3) is