Answer:
The image of
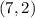 is
is
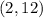
Explanation:
First you need to find the translation vector.
Let the translation vector be
 . Then the translation rule is
. Then the translation rule is
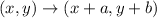 .
.
From the equation, the image of
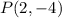 is
is
 .When we apply this rule using the translation vector, we get
.When we apply this rule using the translation vector, we get
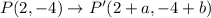
Now we have
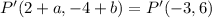
We can therefore equate corresponding coordinates
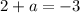 and
and

This implies that:
 and
and

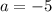 and
and
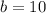
Hence our translation vector is
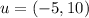
The translation rule now becomes:
 .
.
To find the image of (7,2), we plug it into the translation rule.
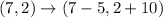 .
.
 .
.