Answer: 0.9730
Explanation:
Let A be the event of the answer being correct and B be the event of the knew the answer.
Given:
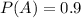
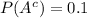
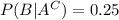
If it is given that the answer is correct , then the probability that he guess the answer
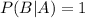
By Bayes theorem , we have
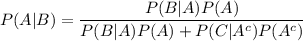
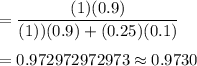
Hence, the student correctly answers a question, the probability that the student really knew the correct answer is 0.9730.