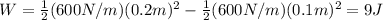Question

Suppose a force of 60 N is required to stretch and hold a spring 0.1 m from its equilibrium position. a. Assuming the spring obeys​ Hooke's law, find the spring constant k. b. How much work is required to compress the spring 0.5 m from its equilibrium​ position? c. How much work is required to stretch the spring 0.6 m from its equilibrium​ position? d. How much additional work is required to stretch the spring 0.1 m if it has already been stretched 0.1 m from its​ equilibrium? a. kequals 600

Answer 1

a. 600 N/m

Hooke's law states that:

F = kx

where

F is the force applied

k is the spring constant

x is the stretching/compression of the spring relative to the equilibrium position

In this problem we have

F = 60 N

x = 0.1 m

So the spring constant is

`x=(F)/(x)=(60 N)/(0.1 m)=600 N/m`

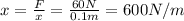
b. 75 J

The work required to stretch a spring is equal to the elastic potential energy stored in the spring:

`W=(1)/(2)kx^2`

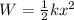
where

k is the spring constant

x is the stretching/compression of the spring

Here we have

k = 600 N/m

x = 0.5 m

So the work done is

`W=(1)/(2)(600 N/m)(0.5 m)^2=75 J`

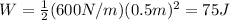
c. 108 J

We can use the same formula used in the previous part:

`W=(1)/(2)kx^2`

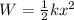
where here we have

k = 600 N/m

x = 0.6 m

So the work done is

`W=(1)/(2)(600 N/m)(0.6 m)^2=108 J`

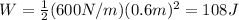
d. 9 J

In this case, the additional work required is the difference between the elastic potential energy in the two situations

`W=(1)/(2)kx_f^2 - (1)/(2)kx_i^2`

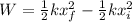
where

k = 600 N/m

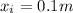`x_i = 0.1 m` is the initial stretching

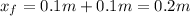`x_f = 0.1 m + 0.1 m = 0.2 m` is the final stretching

Solving the equation,

`W=(1)/(2)(600 N/m)(0.2 m)^2 - (1)/(2)(600 N/m)(0.1 m)^2=9 J`