Answer:
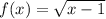 -----> Graph C
-----> Graph C
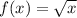 -----> Graph A
-----> Graph A
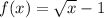 -----> Graph B
-----> Graph B
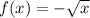 -----> Graph D
-----> Graph D
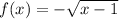 -----> Graph E
-----> Graph E
Explanation:
we have
case a)
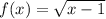
Find the domain
we know that
The radicand must be greater than or equal to zero
so
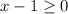
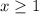
The domain is the interval -----> [1,∞)
All real numbers greater than or equal to 1
The range is the interval -----> [0,∞)
All real numbers greater than or equal to 0
case b)
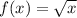
Find the domain
we know that
The radicand must be greater than or equal to zero
so
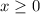
The domain is the interval -----> [0,∞)
All real numbers greater than or equal to 0
The range is the interval -----> [0,∞)
All real numbers greater than or equal to 0
case c)
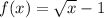
Find the domain
we know that
The radicand must be greater than or equal to zero
so
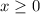
The domain is the interval -----> [0,∞)
All real numbers greater than or equal to 0
The range is the interval -----> [-1,∞)
All real numbers greater than or equal to -1
case d)
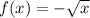
Find the domain
we know that
The radicand must be greater than or equal to zero
so
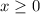
The domain is the interval -----> [0,∞)
All real numbers greater than or equal to 0
The range is the interval -----> (-∞,0]
All real numbers less than or equal to 0
case e)
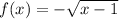
Find the domain
we know that
The radicand must be greater than or equal to zero
so
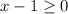
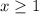
The domain is the interval -----> [1,∞)
All real numbers greater than or equal to 1
The range is the interval -----> (-∞,0]
All real numbers less than or equal to 0