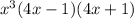Question

Factor the following expression completely. 16x^5-x^3

A.

B.

C.

D.

Answer 1

x^3(2x+1)(2x-1)

Explanation:

first take common then use formula of a^2-b^2

Answer 2

The factor of the provided expression are:
`x^3(4x-1)(4x+1)`

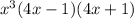
Explanation:

Consider the provided expression.

`16x^5-x^3`

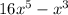
Here the Greatest common factor in the above expression is x³.

The above expression can be written as:

`x^3(16x^2-1)`

`x^3((4x)^2-1^2)`

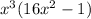
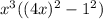
Now use the difference of the square property:
`a^2-b^2=(a+b)(a-b)`

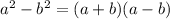
By using the above property we can rewrite the provided expression as shown:

`x^3(4x-1)(4x+1)`

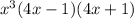
Hence, the factor of the provided expression are:
`x^3(4x-1)(4x+1)`