1 Answer

Ekaqu · Answer 1 · 2020-10-22T16:48:35+0000

The augmented matrix for this system is

$\left[\begin{array}c4&-3&1&22\\4&1&5&30\\3&-1&-1&4\end{array}\right]$

Subtract row 1 from row 2, and subtract 3(row 1) from 4(row 3):

$\left[\begin{array}c4&-3&1&22\\0&4&4&8\\0&5&-7&-50\end{array}\right]$

Multiply row 2 by 1/4:

$\left[\begin{array}ccc4&-3&1&22\\0&1&1&2\\0&5&-7&-50\end{array}\right]$

Subtract 5(row 2) from row 3:

$\left[\begin{array}c4&-3&1&22\\0&1&1&2\\0&0&-12&-60\end{array}\right]$

Multiply row 3 by -1/12:

$\left[\begin{array}c4&-3&1&22\\0&1&1&2\\0&0&1&5\end{array}\right]$

While this isn't exactly RREF, you can already solve the system quite easily:

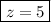
$\boxed{z=5}$

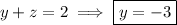
$y+z=2\implies\boxed{y=-3}$

$4x-3y+z=22\implies4x=8\implies\boxed{x=2}$

We can confirm this solution by continuing with the row reduction. Subtract row 3 from row 2:

$\left[\begin{array}c4&-3&1&22\\0&1&0&-3\\0&0&1&5\end{array}\right]$

Subtract -3(row 2) and row 3 from row 1:

$\left[\begin{array}c4&0&0&8\\0&1&0&-3\\0&0&1&5\end{array}\right]$

Finally, multiply row 1 by 1/4:

$\left[\begin{array}c1&0&0&2\\0&1&0&-3\\0&0&1&5\end{array}\right]$

and we end up with
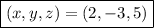$\boxed{(x,y,z)=(2,-3,5)}$ , as before.

Please log in or register to add a comment.