Answer:
D. 13
Explanation:
From the diagram,
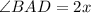 and
and
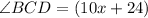
In an isosceles trapezium, the base angles are equal.
This implies that
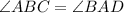
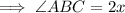
The side length CB of the trapezoid is a transversal line because CD is parallel to AB.
This means that
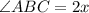 and
and
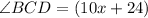 are co-interior angles.
are co-interior angles.
Since co-interior angles are supplementary, we write and solve the following equation for
 .
.
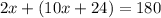
Group similar terms
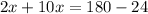
Simplify both sides of the equation.
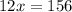
Divide both sides by 12
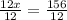
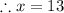
The correct answer is D.