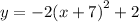ANSWER
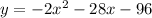
Step-by-step explanation
We have that
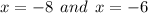
are the roots of the quadratic function.
This implies that
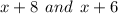
are factors of the quadratic function.
The quadratic function will have an equation of the form:

It was also given that, the vertex of the function is at

This point must satisfy the equation.
This implies that:
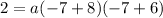
This implies that,
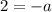
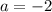
We substitute the value of 'a' to get the equation in factored form as:
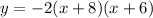
We expand the parenthesis to write the equation in standard form.


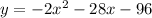
Or in vertex form, the equation is