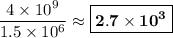Answer:
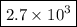
Explanation:
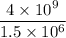
1. Divide the coefficients and the exponentials separately
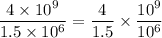
2. Divide the coefficients
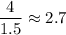
3. Divide the exponential terms
Subtract the exponent in the denominator from the exponent in the numerator.
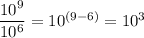
4. Rejoin the new coefficient and the new exponential