Question

What is the length of segment XY?​

Answer 1

7.28 units to the nearest hundredth.

Explanation:

Use the Pythagoras theorem.

If you examine the graph you see that the line segment is the hypotenuse of a right triangle with legs of length 2 and 7.

XY^2 = 2^2 + 7^2

XY^2 = 53

XY = √53

XY = 7.28.

Answer 2

Answer: Third option.

Explanation:

You need to use the formula for calculate the distance between two points. This is:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

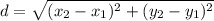
You can observe in the graph that the coordinates of the point X and the point Y are the following:

X(-4,0) and Y(3,2)

Knowing this, you can substitute the coordinates into the formula.

You get that the lenght of the segment XY is:

`d_((XY))=√((3-(-4))^2+(2-0)^2)\\\\d_((XY))=√(53)\ units`

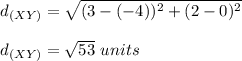
This matches with the third option.