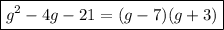Question

Complete the equation to show two equivalent expressions.

g2 – 4g – 21 = (g – )(g + )

Answer 1

Answer: -7 and +3

did the assignment

Answer 2

`g^2-4g-21=(g-7)(g+3)`

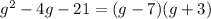
Explanation:

To complete the left side of the equation, we need to bring it to the form

`(g-a)(g+b)`

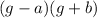
expanding this expression we get:

`g^2+bg-ag-ab`

`g^2+(b-a)g-ab`

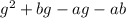
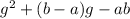
Thus we have

`g^2-4g-21=g^2+(b-a)g-ab`

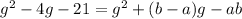
from here we see that for both sides of the equation to be equal, it must be that

`b-a=-4`

`-ab=-21`.

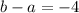
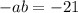Getting rid of the negative signs we get:

`a-b=4`

`ab=21`

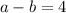
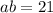
At this point we can either guess the solution to this system (that's how you usually solve these types of problems) or solve for
`a` and
`b` systematically.

The solutions to this set are
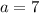`a=7` and
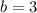`b=3`. (you have to guess on this—it's easier)

Therefore, we have

`(g-a)(g+b)=(g-7)(g+3)`

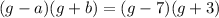
which completes our equation

`\boxed{ g^2-4g-21=(g-7)(g+3)}`