Answer:
One possible function that meets the requirements is
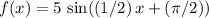 .
.
Explanation:
In general, a sinusoidal function is of the form
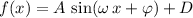 , where
, where
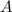 ,
,
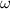 ,
,
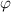 , and
, and
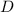 are constants.
are constants.
The constant
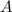 determines the amplitude of this sinusoidal function. The amplitude is
determines the amplitude of this sinusoidal function. The amplitude is
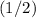 the vertical distance between maxima and minima. In this question, the vertical distance between maxima and minima is
the vertical distance between maxima and minima. In this question, the vertical distance between maxima and minima is
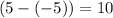 , such that
, such that
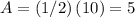 .
.
The constant
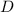 determines the midpoint between maxima and minima. In this question, the midpoint between minima (
determines the midpoint between maxima and minima. In this question, the midpoint between minima (
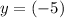 ) and maxima (
) and maxima (
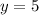 ) is
) is
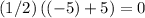 . Hence,
. Hence,
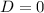 .
.
The constant
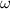 determines the period of this sinusoidal function. The period of
determines the period of this sinusoidal function. The period of
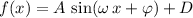 is
is
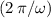 , such that:
, such that:
- the distance between two neighboring maxima would be
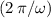 , and
, and - the distance between a maximum and the next minima would be
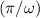 .
.
In this question, assume that there is no minima between
 and
and
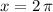 (exclusive). Hence,
(exclusive). Hence,
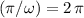 , and
, and
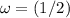 .
.
The constant
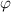 shifts the sinusoidal function horizontally. After finding
shifts the sinusoidal function horizontally. After finding
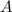 ,
,
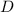 , and
, and
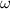 , substitute in a point on the graph of this function to find the value of
, substitute in a point on the graph of this function to find the value of
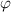 . For example, since
. For example, since
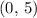 is a point on the graph of
is a point on the graph of
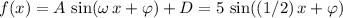 :
:
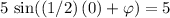 .
.
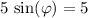 .
.
One possible value of
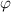 would be
would be
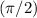 .
.
Hence, one possible formula satisfying the requirements is
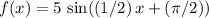 .
.