Question

if y is the midpoint of xz, y is located at (3,-1), and z is located at (11,-5), find the coordinates of x

Answer 1

We define midpoint formula as

`Y(x_m, y_m)=Y((x_2+x_1)/(2), (y_2+y_1)/(2))`

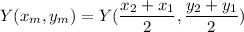
Also here are the coordinates of every point in variables so you won't get confused.

`</p><p>Y(x_m, y_m) \\</p><p>X(x_1, y_1) \\</p><p>Z(x_2, y_2)</p><p>`

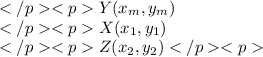
Which means there are two equations. One to find x of point X and one to find y of point X.

`</p><p>x_m=(x_2+x_1)/(2)\Longrightarrow 3=(11+x_1)/(2) \\</p><p>6=11+x_1\Longrightarrow\underline{x_1=-5} \\ \\ </p><p>y_m=(y_2+y_1)/(2)\Longrightarrow-1=(-5+y_1)/(2) \\</p><p>-2=-5+y_1\Longrightarrow\underline{y_1=3}</p><p>`

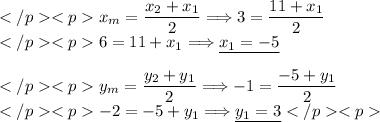
So point X has coordinates:
`\boxed{X(-5, 3)}`

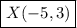
Hope this helps.

r3t40

Answer 2

`\bf ~~~~~~~~~~~~\textit{middle point of 2 points } \\\\ X(\stackrel{x_1}{x}~,~\stackrel{y_1}{y})\qquad Z(\stackrel{x_2}{11}~,~\stackrel{y_2}{-5}) \qquad \left(\cfrac{ x_2 + x_1}{2}~~~ ,~~~ \cfrac{ y_2 + y_1}{2} \right) \\\\\\ \left(\cfrac{11+x}{2}~~,~~\cfrac{-5+y}{2} \right)=\stackrel{\stackrel{midpoint}{y}}{(3,-1)}\implies \begin{cases} \cfrac{11+x}{2}=3\\[1em] 11+x=6\\ \boxed{x=-5}\\ \cline{1-1} \cfrac{-5+y}{2}=-1\\[1em] -5+y=-2\\ \boxed{y=3} \end{cases}`