Question

The hypotenuse of a 45°-45°-90° triangle measures 128 cm. What is the length of one leg of the triangle? 64 cm cm 128 cm cm

Answer 1

Length of one leg of the given triangle will be 64√2 cm.

Explanation:

Length of the hypotenuse of a 45°- 45°- 90° triangle has been given as 128 cm.

Since two angles other than 90° are of same measure so other two sides of the triangle will be same in measure.

Therefore, by Pythagoras theorem,

Hypotenuse² = Leg(1)² + Leg(2)²

Let the measure of both the legs is x cm

(128)² = 2x²

16384 = 2x²

x² =
`(16384)/(2)`

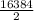
x² = 8192

x = √8192

= 64√2 cm

Therefore, length of one leg of the given triangle will be 64√2 cm.

Answer 2

Answer 64*sqrt(2)

Explanation:

Givens

c = 128 cm

a = b = ??

formula

a^2 + b^2 = c^2 combine the two equal legs.

2a^2 = c^2 Substitute 128 for c

2a^2 = 128^2 Square

2a^2 = 16384 Divide by 2

a^2 = 16384/2

a^2 = 8192 Factor (8192)

8192 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 count the 2s

8192 = 2^13 Break 13 into 2 equal values with 1 left over

sqrt(8192) = sqrt(2^6 * 2^6 * 2^1)

sqrt(8192) = 2^6 * sqrt(2)

The length of one leg is 64*sqrt(2)