Question

The unit cost, in dollars, to produce bins of cat food is $3 and the fixed cost is $6972. The price-demand function, in dollars per bin, is

p

(

x

)

=

253

−

2

x

Find the cost function.

C

(

x

)

=


syntax error

Find the revenue function.

R

(

x

)

=


syntax error

Find the profit function.

P

(

x

)

=


syntax error

At what quantity is the smallest break-even point?

Answer 1

Revenue , Cost and Profit Function

Explanation:

Here we are given the Price/Demand Function as

P(x) = 253-2x

which means when the demand of Cat food is x units , the price will be fixed as 253-2x per unit.

Now let us revenue generated from this demand i.e. x units

Revenue = Demand * Price per unit

R(x) = x * (253-2x)

=
`253x-2x^2`

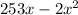
Now let us Evaluate the Cost Function

Cost = Variable cost + Fixed Cost

Variable cost = cost per unit * number of units

= 3*x

= 3x

Fixed Cost = 6972 as given in the problem.

Hence

Cost Function C(x) = 3x+6972

Let us now find the Profit Function

Profit = Revenue - Cost

P(x) = R(x) - C(x)

=
`253x-2x^2 - (3x+6972)\\253x-2x^2-3x-6972\\253x-3x-2x^2-6972\\250x-2x^2-6972\\-2x^2+250x-6972\\`

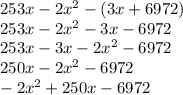
Now we have to find the quantity at which we attain break even point.

We know that at break even point

Profit = 0

Hence P(x) = 0

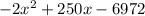`-2x^2+250x-6972`=0

now we have to solve the above equation for x

`-2x^2+250x-6972 = 0`

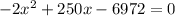
Dividing both sides by -2 we get

`x^2-125x+3486 = 0\\`

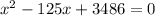
Now we have to find the factors of 3486 whose sum is 125. Which comes out to be 42 and 83

Hence we now solve the above quadratic equation using splitting the middle term method .

`x^2-42x-83x+3486 = 0\\x(x-42)-83(x-43)=0\\(x-42)(x-83)=0\\`

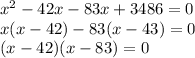
Hence

Either (x-42) = 0 or (x-83) = 0 therefore

if x-42= 0 ; x=42

if x-83=0 ; x=83

Smallest of which is 42. Hence the number of units at which it attains the break even point is 42.