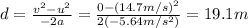Question

Question Part Points Submissions Used A car is traveling at 53.0 km/h on a flat highway. (a) If the coefficient of friction between road and tires on a rainy day is 0.115, what is the minimum distance in which the car will stop? Incorrect: Your answer is incorrect. m (b) What is the stopping distance when the surface is dry and the coefficient of friction is 0.575? m

Answer 1

(a) 95.9 m

The initial velocity of the car is

`u=53.0 km/h = 14.7 m/s`

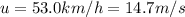
The car moves by uniformly accelerated motion, so we can use the SUVAT equation:

`v^2 - u^2 = 2ad`

where

v = 0 is the final velocity

d is the stopping distance of the car

a is the acceleration of the car

The force of friction against the car is

`F_f = - \mu mg`

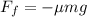
where

`\mu=0.115` is the coefficient of friction

m is the mass of the car

`g = 9.8 m/s^2` is the acceleration due to gravity

According to Newton's second law, the acceleration is

`a=(F)/(m)=(-\mu mg)/(m)=-\mu g`

Substituting into the previous equation:

`v^2 - u^2 = -2\mu g d`

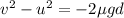
and solving for d:

`d=(v^2 -u^2)/(-2\mu g)=(0-(14.7 m/s)^2)/(-2(0.115)(9.8 m/s^2))=95.9 m`

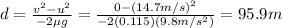
(b) 19.1 m

This time, the coefficient of friction is

`\mu = 0.575`

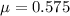
So the acceleration due to friction is:

`a=-\mu g = -(0.575)(9.8 m/s^2)=-5.64 m/s^2`

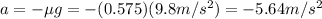
And substituting into the SUVAT equation:

`v^2 - u^2 = 2ad`

we can find the new stopping distance:

`d=(v^2 -u^2)/(-2a)=(0-(14.7 m/s)^2)/(2(-5.64 m/s^2))=19.1 m`