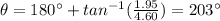Question

A resultant vector is 5 units long and makes an angle of 23 degrees measured counter-clockwise with respect to the positive x-axis. What are the magnitude and angle (measured counter-clockwise with respect to the positive x-axis) of the equilibrant vector?

Answer 1

5 units at 203 degrees

Step-by-step explanation:

The equilibrant vector must have components that are opposite to those of the initial vector.

The components of the initial vector are:

`v_x = v cos \theta = 5 cos 23^(\circ)=4.60\\v_y = v sin \theta = 5 sin 23^(\circ) = 1.95`

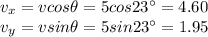
So the components of the equilibrant vector must be

`v_x = -4.60\\v_y = -1.95`

which means its magnitude is

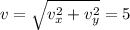`v=√(v_x^2 + v_y^2)= 5` (same magnitude as the initial vector)

and it is located in the 3rd quadrant, so its angle will be

`\theta = 180^(\circ) + tan^(-1) ((1.95)/(4.60))=203^(\circ)`