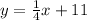Question

A walking path across a park is represented by the equation y= -4x - 6 . A new path will be built perpendicular to this path. The path will intersect at the point (-4 , 10) . Identify the equation that represents the new path .

Answer 1

y=1/4 x +11

Explanation:

So this is a word problem but it isn't too bad to figure what they want: They are looking for a line that is perpendicular to y=-4x-6 and goes through (-4,10).

So we are looking for an equation whose slope is the opposite reciprocal of the given equation's slope.

The given equation has a slope of -4

The opposite reciprocal of -4 is 1/4 so that is the slope of our new line.

So we know our equation is in the form of y=1/4 x+b

Now we are given that this line should go through (-4,10) so plug it in to find b.

10=1/4 * (-4)+b

10=-1+b

11=b

So the equation is y=1/4 x+11

Answer 2

Answer:
`y=(1)/(4)x+11`

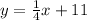
Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Given the equation of the line
`y= -4x - 6`, you can identify that the slope is:

`m=-4`

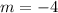
By definition, the slopes of perpendicular lines are negative reciprocals, then the slope of equation of the line that represents the new path which will be built perpendicular to other path, is:

`m=(1)/(4)`

Knowing that the path will intersect at the point (-4 ,10), you need to substitute the slope and this point into
`y=mx+b` and solve for "b":

`10=(1)/(4)(-4)+b\\\\10+1=b\\\\b=11`

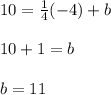
Therefore, the equation that represents the new path is:

`y=(1)/(4)x+11`