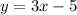Question

What is the rise over run​

Answer 1

Rise over run is another term for slope, with we can use to derive a linear equation.

The term rise over run in technical terms is the change of y over the change of x.

To find the rise over run, subtract the y terms and divide that by the x terms.

`(y_2-y_1)/(x_2-x_1)`

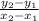
You can use this to derive a linear equation as earlier mentioned by plugging in given points.

For example, a line passes through (3,4) with a rise over run of 3.

`y=mx+b`

`4=3(3)+b`

`4=9+b`

`b=-5`

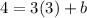
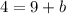
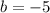
So therefore the y intercept is -5, and the equation is
`y=3x-5`