Answer:
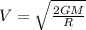
Step-by-step explanation:
Taking into account what is stated in this problem and considering there is no friction during the takeoff of the rocket of the planet, the rocket will escape the gravitational attraction of the massive body when its kinetic energy
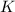 and its potential energy
and its potential energy
 are equal in magnitude.
are equal in magnitude.
Written mathematically is:
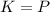 (1)
(1)
Where:
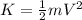 (2)
(2)
Being
 the mass of the rocket
the mass of the rocket
And:
 (3)
(3)
Being
 the mass of the planet,
the mass of the planet,
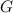 the gravitational constant and
the gravitational constant and
 the radius of the planet.
the radius of the planet.
Substituting (2) and (3) in (1):
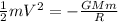 (4)
(4)
Finding
 , which is the escape velocity:
, which is the escape velocity:
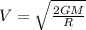 this is the velocity the rocket must have in order to escape from the surface of the planet
this is the velocity the rocket must have in order to escape from the surface of the planet