Question

What is the following quotient?
sqr root 6 + sqr root 11/ sqr root 5+ sqr root 3

Answer 1

The answer is B, the second choice.

Answer 2

`(√(30)-3√(2)+√(55)-√(33) )/(2)`

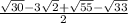
Explanation:

The given expression is

`(√(6)+√(11))/(√(5)+√(3) )`

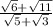
To solve this quotient, we just have to apply a rationalization, which consists in eliminating every root in the denominator. To do so, we multiply and divide the expression by the opposite binomial of the denominator, as follows

`(√(6)+√(11))/(√(5)+√(3) )=(√(5)-√(3) )/(√(5)-√(3) )\\\\((√(6)+√(11))(√(5)-√(3)))/((√(5)+√(3))(√(5)-√(3)))\\\\(√(30)-√(18)+√(55)-√(33) )/(5-3)\\ \\(√(30)-3√(2)+√(55)-√(33) )/(2)`

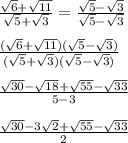
Therefore, the right answer is the second option.