Answer:
(- 1, 0), (9, 0)
Explanation:
The equation of a parabola in vertex form is
y = a(x - h)² + k
where (h, k) are the coordinates of the vertex and a is a multiplier
here (h, k) = (4, 75), so
y = a(x - 4)² + 75
To find a substitute (0, 27) into the equation
27 = a(- 4)² + 75 , that is
27 = 16a + 75 ( subtract 75 from both sides )
16a = - 48 ( divide both sides by 16 )
a = - 3, thus
y = - 3(x - 4)² + 75 ← equation in vertex form
To obtain the x- intercepts let y = 0
- 3(x - 4)² + 75 = 0 ( subtract 75 from both sides )
- 3(x - 4)² = - 75 ( divide both sides by - 3 )
(x - 4)² = 25 ( take the square root of both sides )
x - 4 = ±
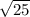 = ± 5
= ± 5
Add 4 to both sides
x = 4 ± 5, hence
x = 4 - 5 = - 1 or x = 4 + 5 = 9
Substitute these values into the equation for corresponding values of y
x = - 1 : y = - 3(- 5)² + 75 = - 75 + 75 = 0 → (- 1, 0)
x = 9 : y = - 3(5)² + 75 = = 75 + 75 = 0 → (9, 0)
The x- intercepts are (- 1, 0), (9, 0)