Answer:
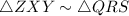
Explanation:
in the given picture , we have two triangles ΔXYZ and ΔRSQ, in which
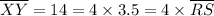
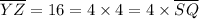
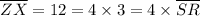
i.e.
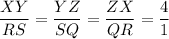
By SSS-similarity postulate, we get
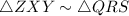
SSS-similarity postulate says that if the lengths of the corresponding sides of two triangles are proportional, then the triangles must be similar