1 Answer

Katiria · Answer 1 · 2020-01-22T21:58:24+0000

Answer:

A.
$y\le2x^2-8x+3$

Explanation:

The given parabola has vertex at (2,-5).

The equation of this parabola in vertex form is given by:

y=a(x-h)^2+k , where (h,k)=(2,-5) is the vertex of the parabola.

We substitute the values to get:

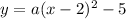
y=a(x-2)^2-5

The graph passes through; (0,3).

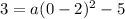
3=a(0-2)^2-5

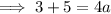
$\implies 3+5=4a$

$\implies 8=4a$

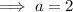
$\implies a=2$

Hence the equation of the parabola is

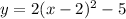
y=2(x-2)^2-5

We expand this to get:

y=2x^2-8x+8-5

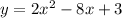
y=2x^2-8x+3

Since the outward region was shaded, the corresponding inequality is

$y\le2x^2-8x+3$

The correct answer is A

Please log in or register to add a comment.