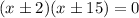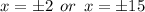Question

If the squared difference of the zeroes of the quadratic polynomial x2+kx+30 is equal to 169 find the value of k and the zeroes

Answer 1

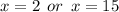
`x = 2 \: \: or \: \: x = 15`

Or

`x = - 2 \: \: or \: \: x = - 15`

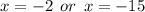
Step-by-step explanation

The given polynomial is

`f(x) = {x}^(2) + kx + 30`

where a=1,b=k, c=30

Let the zeroes of this polynomial be m and n.

Then the sum of roots is

`m + n = - (b)/(a) = -k`

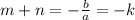
and the product of roots is

`mn = (c)/(a) = 30`

The square difference of the zeroes is given by the expression.

`( {m - n})^(2) = {(m + n)}^(2) - 4mn`

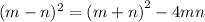
From the question, this difference is 169.

This implies that:

`( { - k)}^(2) - 4(30) = 169`

`{ k}^(2) -120= 169`

`k^(2) = 289`

`k= \pm √(289)`

`k= \pm17`

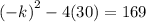
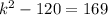
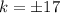
We substitute the values of k into the equation and solve for x.

`f(x) = {x}^(2) \pm17x + 30`

`f(x) = (x \pm2)(x \pm 15)`

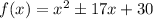
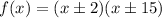
The zeroes are given by;

`(x \pm2)(x \pm 15) = 0`

`x = \pm2 \: \: or \: \: x = \pm 15`