Question

Which statement is true about "f(x)"

The graph of f(x) has a vertex of (–4, 6).
The graph of f(x) is horizontally stretched.
The graph of f(x) opens upward.
The graph of f(x) has a domain of x greater than -6

Answer 1

Answer: Second Option

The graph of f(x) is horizontally stretched.

Explanation:

We have the function:

`f(x) = -(2)/(3)|x+4| - 6`

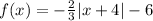
The main function
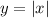`y=|x|` has its vertex in the point (0,0) opens upwards and its domain is all real numbers.

Notice that
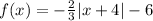`f(x) = -(2)/(3)|x+4| - 6` is a transformation of the function
`y=|x|`.

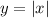Observe the attached image. Where the red line represents the transformed function. Notice that it opens down and is stretched horizontally. Its vertex is at point (4, -6) and the domain is all real numbers

Therefore the statement that is true is the second

The graph of f(x) is horizontally stretched.

Answer 2

The graph of f(x) is horizontally stretched.

EXPLANATION

The given function is

`f(x) = - (2)/(3) |x + 4| - 6`

The vertex of this function is (-4,-6)

The factor ⅔ strectches the graph horizontally in the graph of f(x) opens wider than the parent function

y=|x|

The negative factor will make the graph open downwards. It is a reflection in the x-axis.

The domain of the graph is all real numbers.