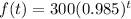Question

What will be the simple interest earned when you invest $1,000 for 3 years at 10 percent and the compound interest earned when you invest the same sum for 2 years at 5 percent ?

The simple interest earned when you invest $1,000 for 3 years at 10 % is $
. The interest compounded when you invest the same sum for 2 years at 5 % is $
.






There are 7 trout fish in a pond,
and the population doubles every year.
Find the population after t years.
arrowBoth

A company buys a machine for $3,000.
The value of the machine depreciates
by 7% every year. Find the value of
the machine after t years.
arrowBoth

The initial population of a colony of ants
is 300. The number of ants increases
at a rate of 1.5% every month. Find the
population of ants after t months.
arrowBoth

A research laboratory is testing a new
vaccine on 300 infected cells. The decay
rate is 1.5% per minute. Find the
number of infected cells after t minutes.
arrowBoth

Answer 1

Part 1) The simple interest earned when you invest $1,000 for 3 years at 10 % is $300

Part 2) The interest compounded when you invest the same sum for 2 years at 5 % is $102.50

Part 3)
`f(t)=7(2)^t`

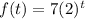
Part 4)
`f(t)=3,000(0.93)^t`

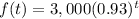
Part 5)
`f(t)=300(1.015)^t`

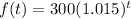
Part 6)
`f(t)=300(0.985)^t`

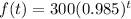
Explanation:

Part 1) What will be the simple interest earned when you invest $1,000 for 3 years at 10 percent

we know that

The simple interest formula is equal to

`I=P(rt)`

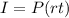
where

I is the Final Interest Value

P is the Principal amount of money to be invested

r is the rate of interest

t is Number of Time Periods

in this problem we have

`t=3\ years\\ P=\$1,000\\r=0.10`

substitute in the formula above

`I=\$1,000(0.10*3)=\$300`

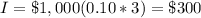
Part 2) What will be the compound interest earned when you invest $1,000 for 2 years at 5 percent ?

we know that

The compound interest formula is equal to

`A=P(1+(r)/(n))^(nt)`

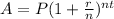
where

I is the Final Investment Value

P is the Principal amount of money to be invested

r is the rate of interest in decimal

t is Number of Time Periods

n is the number of times interest is compounded per year

in this problem we have

`t=2\ years\\ P=\$1,000\\ r=0.05\\n=1`

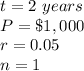
substitute in the formula above

`A=\$1,000(1+(0.05)/(1))^(1*2)`

`A=\$1,000(1.05)^(2)=\$1,102.50`

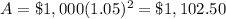
The interest is equal to

`I=\$1,102.50-\$1,000=\$102.50`

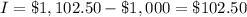
Part 3) There are 7 trout fish in a pond, and the population doubles every year.

Find the population after t years.

we know that

This question is about exponent function of the form

`f(x)= a(b)^t`

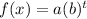
where

a is the initial value

b is the base of the exponent.

In this problem we have

There are 7 trout fish in the pound ----> initial value a=7

The population is double every year ------> the base is b=2

substitute

`f(t)= 7(2)^t`

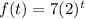
Part 4) A company buys a machine for $3,000. The value of the machine depreciates by 7% every year. Find the value of the machine after t years.

we know that

This question is about exponent function of the form

`f(x)= a(b)^t`

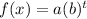
where

a is the initial value

b is the base of the exponent.

we have

Company buys a machine for $3,000 --> initial value is a=3,000

The value depreciate 7% a year

Since it was decreased by 7% every year, it will become: 100%-7%=93%

the base is 93%, b=0.93

substitute

`f(t)=3,000(0.93)^t`

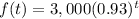
Part 5) The initial population of a colony of ants is 300. The number of ants increases at a rate of 1.5% every month. Find the population of ants after t months.

we know that

This question is about exponent function of the form

`f(x)= a(b)^t`

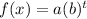
where

a is the initial value

b is the base of the exponent.

we have

Initial population of ants is 300----> initial value is a=300

The number of ants increases 1.5% per month.

Since it will increases by 1.5% every month, it will become: 100%+1.5%=101.5%

the base is 101.5%, b=1.015

substitute

`f(t)=300(1.015)^t`

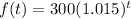
Part 6) A research laboratory is testing a new vaccine on 300 infected cells. The decay rate is 1.5% per minute. Find the number of infected cells after t minutes.

we know that

This question is about exponent function of the form

`f(x)= a(b)^t`

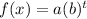
where

a is the initial value

b is the base of the exponent.

we have

A research laboratory is testing new vaccine on 300 infected cells

initial value is a=300

The decay/decrease rate is 1.5% per minute

Since it will decrease by 1.5% every min, it will become: 100%-1.5%=98.5%

the base is 98.5%, b=0.985

substitute

`f(t)=300(0.985)^t`