Answer:
Explanation:
This is right triangle trig. The reference angle is 12 in one case and 60 in the other, but the horizontal distance doesn't change in either one, and neither does what you are looking for, which is the height of the balloon in both cases of the angle differences. And if you're looking for the difference in the height, you'll find both and subtract the smaller from the larger.
The height is across from the reference angle and the horizontal distance is adjacent to the reference angle, so the trig identity you want is tangent. Set up according to the angle measure of 12 degrees:
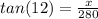 and
and
280 tan(12) = x
x = 59.5 ft
Now for the angle measuring 60 degrees:
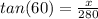 and
and
280 tan(60) = x
x = 484.9
The difference between the two heights is 425.5 feet.