Answer: 10615 nm
Step-by-step explanation:
This problem can be solved by the Wien's displacement law, which relates the wavelength
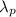 where the intensity of the radiation is maximum (also called peak wavelength) with the temperature
where the intensity of the radiation is maximum (also called peak wavelength) with the temperature
 of the black body.
of the black body.
In other words:
There is an inverse relationship between the wavelength at which the emission peak of a blackbody occurs and its temperature.
Being this expresed as:
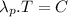 (1)
(1)
Where:
 is in Kelvin (K)
is in Kelvin (K)
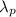 is the wavelength of the emission peak in meters (m).
is the wavelength of the emission peak in meters (m).
 is the Wien constant, whose value is
is the Wien constant, whose value is
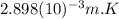
From this we can deduce that the higher the black body temperature, the shorter the maximum wavelength of emission will be.
Now, let's apply equation (1), finding
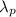 :
:
 (2)
(2)
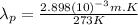
Finally:
 This is the peak wavelength for radiation from ice at 273 K, and corresponds to the infrared.
This is the peak wavelength for radiation from ice at 273 K, and corresponds to the infrared.