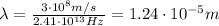Question

About 0.1 eV is required to break a "hydrogen bond" in a protein molecule. Calculate the minimum frequency and maximum wavelength of a photon that can accomplish this.

minimum frequency
Hz
maximum wavelength
m

Answer 1

`2.41\cdot 10^(13)Hz, 1.24\cdot 10^(-5)m`

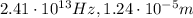
Step-by-step explanation:

The energy of the photon must be equal to 0.1 eV, so let's convert this value into Joules first:

`E=0.1 eV \cdot 1.6\cdot 10^(-19) J=1.6\cdot 10^(-20)J`

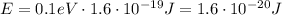
The energy of the photon is related to its frequency by

`E=hf`

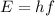
where h is the Planck constant and f is the frequency. Substituting,

`f=(E)/(h)=(1.6\cdot 10^(-20)J)/(6.63\cdot 10^(-34)Js)=2.41\cdot 10^(13)Hz`

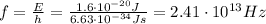
And now we can find the wavelength of the photon, which is given by

`\lambda=(c)/(f)`

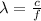
where c is the speed of light. Substituting,

`\lambda=(3\cdot 10^8 m/s)/(2.41\cdot 10^(13) Hz)=1.24\cdot 10^(-5)m`