Question

PLEASE HELP!
Questions are in attachment below :)

Answer 1

Explanation:

1 option 2c

Answer 2

1. The equation of a circle with center (h,k) and radius r units is given by

`(x-h)^2+(y-k)^2=r^2`

The given circle has center (5,-2) and a radius r=3 units.

We substitute these values into the formula to get:

`(x-5)^2+(y--2)^2=3^2`

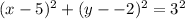
This simplifies to:

`(x-5)^2+(y+2)^2=9`

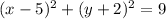
The correct answer is A.

2. The given circle has center (3,-5) and radius r=8 units.

We substitute the given values into the formula to obtain:

`(x-3)^2+(y--5)^2=8^2`

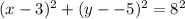
We simplify to get:

`(x-3)^2+(y+5)^2=64`

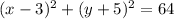
The correct answer is C

3. The given circle has equation:

`(x+8)^2+(y+9)^2=169`

We can rewrite this equation as:

`(x--8)^2+(y--9)^2=13^2`

Comparing this to

`(x-h)^2+(y-k)^2=r^2`

The center is (-8,-9) and the radius is 13.

The correct answer is A.

4. The given circle has equation:

`(x-7)^2+y^2=225`

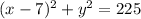
We can rewrite this equation as:

`(x-7)^2+(y-0)^2=15^2`

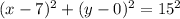
Comparing this to

`(x-h)^2+(y-k)^2=r^2`

The center is (7,0) and the radius is 15.

The correct answer is B.

5. The given circle has center (-2,6) and passes through (-2,10).

We can use the number line to find the radius.

`r=|10-6|=4`

`(x-h)^2+(y-k)^2=r^2`

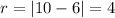
We substitute the center and the radius into the formula to get:

`(x--2)^2+(y-6)^2=4^2`

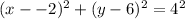
This simplifies to:

`(x+2)^2+(y-6)^2=16`

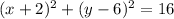
The correct answer is A

6. The given circle has center (1,2) and passes through (0,6).

We can use the distance formula to find the radius.

`r=√((1-0)^2+(2-6)^2)=√(17)`

`(x-h)^2+(y-k)^2=r^2`

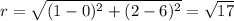
We substitute the center and the radius into the formula to get:

`(x-1)^2+(y-2)^2=√(17)^2`

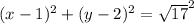
This simplifies to:

`(x-1)^2+(y-2)^2=17`

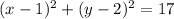
The correct answer is C