Answer:
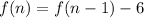 , where
, where
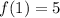 and
and

Explanation:
The terms of the sequence are:
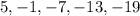
The first term of this sequence is
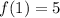 .
.
There is a constant difference among the terms.
This constant difference can determined by subtracting a previous term from a subsequent term.

The general term of this arithmetic sequence is given recursively by
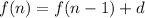
We substitute the necessary values to obtain:
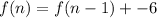
Or
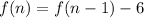 , where
, where
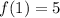 and
and
