Question

Select the correct statement

Answer 1

B

Explanation:

Answer 2

Based on the exponential function,
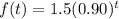`f(t)=1.5(0.90)^t`, the correct statement include the following: B. The number of employees is decreasing by 10% every year.

How to determine the population of bacteria after 4 days?

In Mathematics and Statistics, a population that decreases at a specific period of time represent an exponential decay.

This ultimately implies that, a mathematical model for any population that decreases by r percent per unit of time is an exponential function of this form:

`P(t) = I(1 - r)^t`

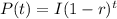
Where:

• P(t ) represents the final population.
• t represents the time or number of years or days.
• I represents the initial population.
• r represents the decay rate.

By comparing the exponential function that models the number of employees with the standard form, the decay rate can be calculated as follows;

1 - r = 0.90

Decay rate, r = 1 - 0.90

Decay rate, r = 0.10

In order to conver the value into percentage, we would multiply by 100;

Decay rate, r = 0.10 × 100

Decay rate, r = 10%.