Answer: 0.001
Explanation:
Binomial probability formula :
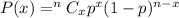 , where P(x) is the probability of exactly x successes in n trials.
, where P(x) is the probability of exactly x successes in n trials.
Given : The probability of city workers take the bus to work =15%=0.15
The sample size :n= 10
Now, the probability that exactly 6 put of 10 workers take the bus to work :-
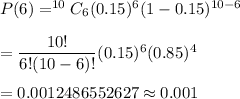
Therefore , the probability that exactly 6 workers take the bus to work = 0.001