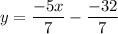Question

Write the equation of a line that is perpendicular to y=7/5x+ 6 and that passes through the point (2,-6).

Answer 1

Given that,

The equation of line is y=7/5x+ 6 and that passes through the point (2,-6).

To find,

The equation of line that is perpendicular to the given line.

Solution,

The given line is :

y=7/5x+ 6

The slope of this line = 7/5

For two perpendicular lines, the product of slopes of two lines is :

`m_1m_2=-1\\\\m_2=(-1)/(7/5)\\\\=(-5)/(7)`

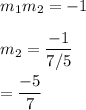
Equation will be :

y=-5x/7+ b

Now finding the value of b. As it passes through (2,-6). The equation of line will be :

`-6=(-5)/(7)(2)+b\\\\ -6=(-10)/(7)+b\\\\b=-6+(10)/(7)\\\\b=(-32)/(7)`

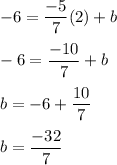
So, the required equation of line is :

y=-5x/7+ (-32/7)

`y=(-5x)/(7)-(-32)/(7)`