Question

Type the correct answer in each box. If necessary, round your answers to the nearest hundredth.

The vertices of ∆ABC are A(2, 8), B(16, 2), and C(6, 2). The perimeter of ∆ABC is

units, and its area is

square units.

Answer 1

30 square units

Explanation:

Answer 2

Perimeter = 32.44 units

Area = 30 square units

Explanation:

Given

Vertices

A(2,8), B(16,2) and C(6,2)

WE have to determine the lengths of all sides before finding the perimeter and area.

The formula of modulus is:

`d = \sqrt{(x_(2)- x_(1))^(2) +(y_(2)-y_(1))^(2)}\\AB=\sqrt{(16-2)^(2) +(2-8)^(2)}\\=\sqrt{(14)^(2) +(-6)^(2)}\\=√(196+36)\\ =√(232)\\=15.23\\\\BC=\sqrt{(6-16)^(2) +(2-2)^(2)}\\=\sqrt{(-10)^(2) +(0)^(2)}\\=√(100+0)\\ =√(100)\\=10\\\\AC=\sqrt{(6-2)^(2) +(2-8)^(2)}\\=\sqrt{(4)^(2) +(-6)^(2)}\\=√(16+36)\\ =√(52)\\=7.21\\\\`

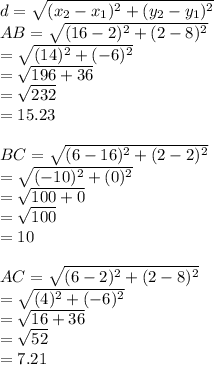
So the perimeter is:

`Perimeter=AB+BC+AC\\=15.23+10+7.21\\=32.44\ units`

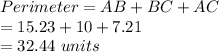
Using hero's formula,

`s=(perimeter)/(2)\\s=(32.44)/(2)\\ s=16.22\\Area=√(s(s-a)(s-b)(s-c))\\=√(16.22(16.22-15.23)(16.22-10)(16.22-7.21))\\=√((16.22)(0.99)(6.22)(9.01))\\=√(899.91)\\=29.99\ square\ units`

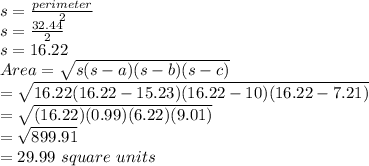
Rounding off will give us 30 square units ..