Question

What is the domain and range for the following function and its inverse?

f(x) = x2 + 3

f(x)
domain:
f–1(x)
domain:

Answer 1

Explanation:

The domain of that function is all real numbers. The x values will drop into negative infinity and will grow to positive infinity.

The range is found from the vertex form of a parabola, which is

`y=(x-h)^2+k`

where h indicates side to side movement of the vertex and k indicates up or down. Our function has a +3 at the end of it and is positive (so it opens upwards), so the range is y ≥ 3.

To find the inverse of that function, switch the x and y coordinates and solve for the new y. Let f(x) be y, then switch the x and y:

`x=y^2+3`

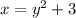
Now solve for the new y:

y = ±
`√(x-3)`

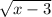
To find the domain of a radical, set the radicand greater than or equal to 0 and solve for x (this is because the radicand cannot be a negative number or we are dealing with imaginary numbers and that's not what you want. BTW, a radicand is the term under the radical sign).

x - 3 ≥ 0 so x ≥ 3. The domain of the inverse is all real numbers greater than or equal to 3.

This is a sideways parabola (the inverse is), and it opens to the right starting at the x value of 3. It will grow into positive values of y to infinity and will drop into negative values of y into negative infinity.

Just a little trick here to remember, and it ALWAYS holds true: the domain of a function is the range of its inverse, and the range of a function is the domain of its inverse. Look to our solution for your problem here and you'll see that it is true.