Answer:
Option A is correct.
Explanation:
Zeros at -8, -1 and 3 means these are the factors of the polynomial.
x=-8, x=-1 and x =3
It can be written as:
x+8=0, x+1=0 and x-3=0
Factors can be written as:
(x+8)(x+1)(x-3)=0
Multiplying the first two terms and then their product with third terms:
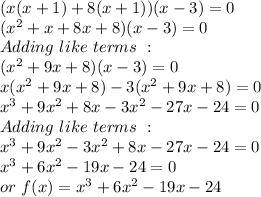
So, Option A is correct.