Question

What is the measure of each interior angle of a regular polygon with 5 sides?

Answer 1

108 degrees because of the equation 180(n-2)/n. 180(5-2)/5= 540/5= 108.

Answer 2

108°

Step-by-step explanation

The measure of each interior angle of a regular polygon is given by

`\theta = ((n - 2) * 180)/(n)`

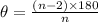
where n refers to the number of sides of the polygon.

From the question we have n=5 in this case.

We substitute to obtain;

`\theta = ((5 - 2) * 180)/(5)`

`\theta = (3* 36)/(1)`

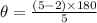
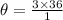
This simplifies to:

`\theta = 108 \degree`

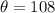
Hence each interior angles of a regular polygon with 5 - sides is 108°