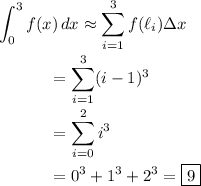Split up the interval [0, 3] into 3 equally spaced subintervals of length
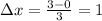 . So we have the partition
. So we have the partition
[0, 1] U [1, 2] U [2, 3]
The left endpoint of the
 -th subinterval is
-th subinterval is
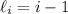
where
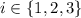 .
.
Then the area is given by the definite integral and approximated by the left-hand Riemann sum