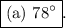In a circle, if arc AB measures 104° and arc CD measures 26°, the inscribed angle BPA, intercepted by arc AB, is half the arc's measure, resulting in a ∠BPA of 52°. Additionally, exterior ∠BPD is 78°, making the correct answer (a) 78°.
To find the measure of angle BPA in the circle, we can use the fact that the measure of an inscribed angle is half the measure of its intercepted arc.
Let
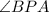 be the inscribed angle, and let
be the inscribed angle, and let
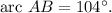 Since
Since
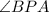 intercepts arc AB, we have:
intercepts arc AB, we have:
![\[ \text{measure of } \angle BPA = \frac{\text{measure of arc } AB}{2} \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/jpcv8z7zrqk0sb8nr2v7.png)
![\[ \text{measure of } \angle BPA = (104^\circ)/(2) = 52^\circ \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/ftrrm2zsmfszmjv47jx1.png)
So, the measure of
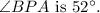
Now, let's look at arc CD. Since C and D are on the other side of the circle,
 is an exterior angle to triangle APB. The measure of an exterior angle is equal to the sum of the measures of the two opposite interior angles.
is an exterior angle to triangle APB. The measure of an exterior angle is equal to the sum of the measures of the two opposite interior angles.
![\[ \text{measure of } \angle BPD = \text{measure of } \angle BPA + \text{measure of arc } CD \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/cl0yt24e4ud459d0d3lb.png)
![\[ \text{measure of } \angle BPD = 52^\circ + 26^\circ = 78^\circ \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/q80kxpg7vbpu9bbr2qlf.png)
So, the measure of

The answer is