Question

g The sixth row of Pascal's Triangle is: 1 6 15 20 15 6 1 (a) What is the 7th row of Pascal's Triangle? (b) Use your answer to the previous problem to write the expanded form of (x + y)7.

Answer 1

a)The 7th row is:

1 7 21 35 35 35 21 7 1

b)

`{(x + y)}^(7) = {x}^(7)+ 7 {x}^(6) y+ 21 {x}^(5) {y}^(2)+ 35 {x}^(4) {y}^(3) + 35{x}^(3) {y}^(4) + 21{x}^(2) {y}^(5) + 7x {y}^(6)+ {y}^(7)`

Step-by-step explanation

The sixth row of Pascal's Triangle is:

1 6 15 20 15 6 1.

We generate the 7th row by repeating the eXtreme 1s and adding the entries directly above to generate the entries within as show in the attachment.

The 7th row is:

1 7 21 35 35 35 21 7 1

b) We can use this to expand

`{(x + y)}^(7)`

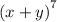
We know that the degree of x is going to decrease from left to right and the degree of y is going to increase from left to right.

`{(x + y)}^(7) = 1 ({x}^(7) ) + 7( {x}^(6) y) + 21( {x}^(5) {y}^(2) ) + 35( {x}^(4) {y}^(3) ) + 35( {x}^(3) {y}^(4) ) + 21( {x}^(2) {y}^(5) ) + 7( x {y}^(6) ) + 1( {y}^(7) )`

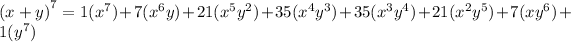
This simplifies to,

`{(x + y)}^(7) = {x}^(7)+ 7 {x}^(6) y+ 21 {x}^(5) {y}^(2)+ 35 {x}^(4) {y}^(3) + 35{x}^(3) {y}^(4) + 21{x}^(2) {y}^(5) + 7x {y}^(6)+ {y}^(7)`