Question

Which of the following represents a quadratic function?

a. y = 3x - 2
b. y=6+5x + x²
c. x³10x = 21
d. y= 2² +4

Answer 1

`\huge\underline{\underline{\boxed{\mathbb {SOLUTION:}}}}`

`\leadsto` A quadratic equation is an algebraic equation of the second degree. The formula is:

▪
`\longrightarrow \sf{y = ax^2 + bx + c}`

This can also be written as:

▪
`\longrightarrow \sf{y = c + bx+ax^2}`

Comparing the equation above with each of the options, the equation that represents a quadratic function is:

`\longrightarrow \sf{y=6+5 + x^2}`

`\huge\underline{\underline{\boxed{\mathbb {ANSWER:}}}}`

◉
`\large\bm{b. \: y=6+5x + x^2}`

Answer 2

○
`y = 6 + 5x + x^2`

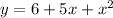
Step-by-step explanation:

What is a quadratic equation?

A quadratic equation is an algebraic equation where the highest power of
`x` is 2. The general form of a quadratic equation is as follows:

`\boxed{ax^2 + bx + c = 0}`,

where a, b, and c represent known constants, and
`x` is the unknown.

In this question, if you take a look at the second option, you will see that it is possible to rearrange the equation to make it look the general form:

`y = 6 + 5x + x^2`

⇒
`y = x^2 + 5x + 6`

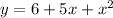
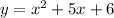
Therefore, this equation is quadratic.

The other three options are not quadratic equations because none of them have an
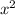`x^2` term in them.