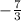Answer:
Explanation:
To solve this, we are using the average rate of change formula:
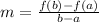
where
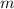 is the average rate of change
is the average rate of change
 is the first point
is the first point
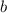 is the second point
is the second point
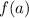 is the function evaluated at the first point
is the function evaluated at the first point
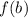 is the function evaluated at the second point
is the function evaluated at the second point
We want to know the average rate of change of the function
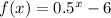 form x = -3 to x = 0, so our first point is -3 and our second point is 0. In other words,
form x = -3 to x = 0, so our first point is -3 and our second point is 0. In other words,
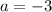 and
and
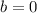 .
.
Replacing values
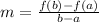
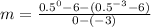
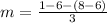
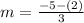
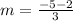
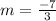
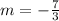
We can conclude that the average rate of change of the exponential equation form x = -3 to x = 0 is