Answer:
1. Domain: The set of natural numbers / Range: The set of natural numbers
2. Shown below
Explanation:
1. Domain and Range.
In this problem, we have that the number of frogs in a certain lake is inversely related to the number of snakes in the lake. Hence we are facing an Inverse Variation, so this means that if the number of snakes in the lake increases then the number of frogs in the lake decreases, because snakes eat frogs! The function that describes this is a rational function defined as:

Where:
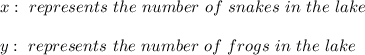
As you can see,
 is in the denominator, therefore
is in the denominator, therefore
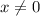 . Since we need to provide a reasonable domain, we say that the domain is the set of natural numbers and this doesn't include the number 0. Why aren't negative values included in the domain as well? Well, although negative values are included in the function, they aren't reasonable because
. Since we need to provide a reasonable domain, we say that the domain is the set of natural numbers and this doesn't include the number 0. Why aren't negative values included in the domain as well? Well, although negative values are included in the function, they aren't reasonable because
 represents the number of snakes and you always get positive numbers when counting things.
represents the number of snakes and you always get positive numbers when counting things.
To get the range, let's take the inverse of this function, so:

So the domain of
 is the range of our given function
is the range of our given function
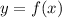 . As you can see the inverse function is the same as our given function, then the range is the set of natural numbers as well.
. As you can see the inverse function is the same as our given function, then the range is the set of natural numbers as well.
2. Graph.
First of all, we can define the pattern of the rational function as:

So our function will be:
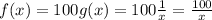
So the graph of
 will be the same graph of
will be the same graph of
 but it's been stretched vertically by a constant of 100, that is, each y-value is multiplied by 100. Also, since
but it's been stretched vertically by a constant of 100, that is, each y-value is multiplied by 100. Also, since
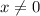 and
and
 then at
then at
 there is a vertical asymptote and at
there is a vertical asymptote and at
 there is an horizontal asymptote. Finally, the graph is shown below for
there is an horizontal asymptote. Finally, the graph is shown below for
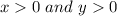 , but remember: Whenever
, but remember: Whenever
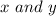 are natural numbers.
are natural numbers.