Answer:
Vertex:
Roots:
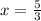 or
or

Explanation:
The given quadratic equation is:
Let
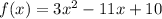
We obtain the vertex form by completing the square;
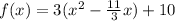
Add and subtract the square of half the coefficient of x.
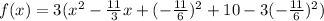
This simplifies to
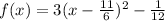
Hence the vertex is
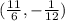
We now solve to obtain:

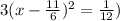
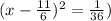
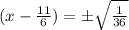
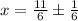
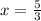 or
or
