Answer:
See attached diagram
Explanation:
You are given the equation of hyperbola
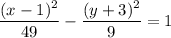
From this equation,
- the center of hyperbola is at point (1,-3);
- the real semi-axes

- the imaginary semi-axes
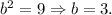
Draw two parallel lines x=1 and y=-3 (they intersect at the center of hyperbola), then on horizontal line match two hyperbola's vertices (7 units to the left and 7 units to the right from the center). Then draw two branches of hyperbola (one in negative direction and one in positive direction).