Question

Find the sum of the geometric series if it exists .... (any responses ASAP my project is due tomorrow)

Answer 1

Final answer is
`(200)/(11)`.

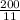Explanation:

Given infinite geometric series is
`20-2+(1)/(5)-\cdot\cdot\cdot`.

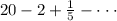First term
`a_1=20`,

Second term
`a_2=-2`,

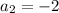Third term
`a_3=(1)/(5)`

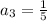
then common ratio using first and 2nd terms

`r=(a_2)/(a_1)=-(2)/(20)=-0.1`

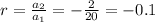
common ratio using 2nd and 3rd term

`r=(a_3)/(a_2)=(\left((1)/(5)\right))/(-2)=-0.1`

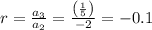
Hence it is confirmed that it is an infinite geometric series

Now plug these values into infinite sum formula of geometric series:

`S_(\infty)=(a_1)/(1-r)=(20)/(1-\left(-0.1\right))=(20)/(1.1)=(200)/(11)`

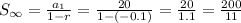
Hence final answer is
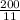`(200)/(11)`.