Question

Which of the following points lies on the graph of f(x) = -x 2?

(-4, 2)
(-2, -4)
(-2, 4)
(4, -2)

Answer 1

(-2, -4)

Explanation:

we have

`f(x)=-x^(2)`

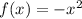
we know that

If a ordered pair lies on the graph, then the ordered pair must satisfy the equation of f(x)

Verify each ordered pair

case A) (-4, 2)

Substitute the value ox x and the value of y in the equation and then compare the results

`2=-(-4)^(2)`

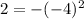
`2=-16` ------> is not true

therefore

The point not lies on the graph

case B) (-2, -4)

Substitute the value ox x and the value of y in the equation and then compare the results

`-4=-(-2)^(2)`

`-4=-4` ------> is true

therefore

The point lies on the graph

case C) (-2, 4)

Substitute the value ox x and the value of y in the equation and then compare the results

`4=-(-2)^(2)`

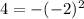
`4=-4` ------> is not true

therefore

The point not lies on the graph

case D) (4, -2)

Substitute the value ox x and the value of y in the equation and then compare the results

`-2=-(4)^(2)`

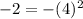
`-2=-16` ------> is not true

therefore

The point not lies on the graph